
Introduction
Dans la plupart des problème de chauffage par induction, la puissance requise est donnée par l'appareillage utilisé, on optimise alors l'ensemble "bobine + échantillon". Soit ici, les dimensions initiales de cet échantillon et la puissance disponible, on cherche à maximiser l'ensemble pour avoir la puissance volumique maximale dans la pièce :
- Données :
- Cible : cylindre aluminium
- Puissance disponible (Pw) : 100 kW
- Fréquence (f) : 60 Hz
- Résistivité aluminium (ρ) : 5.7 µΩ•cm
- Perméabilité aluminium (μ) : 1
- Diamètre cylindre (D) : 7.6 cm (3.0 ")
- Longueur cylindre (L) : 50.8 cm (20 ")
Question / Réponse
- Montrer en conservant le même champ magnétique qu'il existe un rayon pour lequel la puissance volumique dans la cible est maximale.
- Réponse :
On part du modèle défini par les données ci-contre, c'est-à-dire rayon cylindre = 1.5"
(puisque le modèle est axisymétrique) pour lequel on vérifie que la puissance disponible dans la cible
est d'environ 100 kW. Puis on part d'un rayon minimal pour l'augmenter progressivement pour relever :
rayon, volume, pertes par effet Joule (le modèle n'ayant pas d'entrefer toute l'énergie électromagnétique
est considérée comme étant transformée en chaleur).
L'utilisation de
LabelMover
donne :
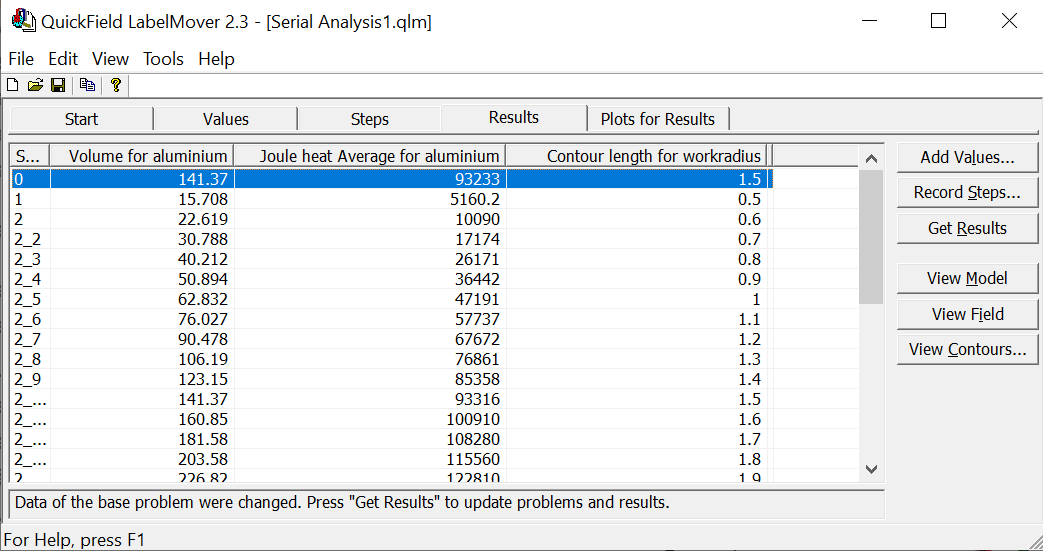
On trouve après calcul Puissance/Volume, un rayon optimum de 1.1" :
Le tableau suivant compare les résultats (A/m), le nombre de noeuds étant < 3 000, la précision est moyenne.
